Tip - Using LLL

Lưu ý tất cả những gì mình viết đều tham khảo từ “Unofficial” - 35C3 CTF. Nếu bạn muốn tìm hiểu thêm, hãy truy cập vào liên kết để có thông tin chi tiết.

LLL là gì

LLL hay gọi là Lenstra-Lenstra-Lovász là thuật toán được sử dụng trên $lattices$.

Nếu như ta có một cơ sở $(basic)$ trong $\mathbb{R}^n$ thì lattices được sinh ra bởi những vector này bao gồm tất cả các tổ hợp nguyên của các vector cơ sở ${b_1, b_2, … b_n}$ trong $\mathbb{R}^n$. Lattice có thể được định nghĩa như sau:

\[L = \{a_1b_1 + a_2b_2 +... + a_nb_n|a_n \in \mathbb{Z}\}\]

Ví dụ, nếu cơ sở của chúng ta là $(1,0)$ và $(0,1)$, thì lattice sinh ra bởi chúng là lưới số nguyên.

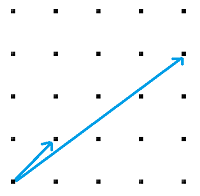
Nếu ta chọn một cơ sở khác cho lattices, ví dụ $(1, 1), (4, 3)$:

Đây thực chất là cùng một lattice nhưng với một cơ sở khác. Có thể thấy rằng chúng giống nhau vì đều cùng tạo ra (1, 0), (0, 1) từ những vector này:

\[(1, 0) = (4, 3) - 3*(1, 1)\] \[(0, 1) = 4*(1, 0) - (4,3)\]

Như vậy ta cũng có thể sinh ra toàn bộ lưới.

LLL là thuật toán mà nhận vào một cơ sở cho một lattice và cố gắng tìm một cơ sở khác “đẹp” hơn và đảm bảo rằng cơ sở mới “nhỏ” nhất có thể.

Ví dụ trên cho thấy rằng nếu ta đưa LLL cơ sở thứ hai thì nó sẽ cố tạo ra một cái gì đó trông giống như cơ sở đầu tiên - vì chúng trông “nhỏ” hơn. Vậy điều này có ý nghĩa gì đối với mật mã học? Giả sử ta mong muốn tìm giá trị bí mật nào đó mà thoả mãn:

$\gt\gt$ Tạo ra một lattice

$\gt\gt$ Giá trị đó nằm trong lattice

$\gt\gt$ Giá trị đó đủ “nhỏ” so với lattice

thì chúng ta có thể sử dụng LLL để tìm nó.

Sử dụng LLL

Xét hệ $i$ phương trình sau: \(k_i = a_i + Xb_i \mod p<2^{128}, p\approx2^{134}\)

\[\Leftrightarrow \exists (\lambda_1, \lambda_2, ..., \lambda_n), k_i = a_i + Xb_i + \lambda_i*p<2^{128}\]

Ta hãy thử biểu diễn ma trận sau với mỗi hàng là một hàng của một cơ sở:

\[\begin{pmatrix} a_1 & a_2 & a_3 & \dots & a_n \\ b_1 & b_2 & b_3 & \dots & b_n \\ p & 0 & 0 & \dots & 0 \\ 0 & p & 0 & \dots & 0 \\ \\ &&&\dots& \\ 0 & 0 & 0 & \dots & p \end{pmatrix}\]

Ở đây, chúng ta kì vọng rằng $a_i, b_i$ cùng số bit với $p$ vì vậy mỗi hàng đều có kích thước ít nhất là 134 bit

Bây giờ, vector sau sẽ nằm trong lattice được sinh ra bởi cơ sở này:

\[(k_1, k_2, ..., k_n)\]

Bởi vì nó là tổng của:

$\gt$ 1 lần hàng $a_i$

$\gt$ X lần hàng $b_i$

$\gt$ $\lambda_i$ lần hàng p

Có thể thấy vector này khá nhỏ$!!!$ Các phần tử của nó chỉ bao gồm 128 bit $\ll$ 134 bits $p$

Vì vậy, chúng ta có một vectơ mà chúng ta muốn tìm (vì nó chứa giá trị $k_i$ cần tìm), nằm trong lattice của chúng ta, và “nhỏ”, nên có thể LLL có thể tìm thấy nó! Tuy nhiên, có hai vấn đề:

• Ta có $i+2$ vectơ ở đó, nhưng các vectơ của chúng ta có $i$ chiều.
• Ta không muốn thêm bất kỳ tổ hợp nào của các vectơ - đảm bảo rằng nó chỉ chọn $1$ cho bội số của hàng đầu tiên.

Ta sẽ khắc phục điều này bằng cách thêm vào hai cột bổ sung cho các vectơ của chúng ta, như sau:

\[\begin{pmatrix} a_1 & a_2 & a_3 & \dots & a_n & ?_A & 0\\ b_1 & b_2 & b_3 & \dots & b_n & 0 & ?_B\\ p & 0 & 0 & \dots & 0 &0 &0\\ 0 & p & 0 & \dots & 0 &0 &0\\ \\ &&&\dots& \\ 0 & 0 & 0 & \dots & p &0&0 \end{pmatrix}\]

Do đó vector mà chúng ta nhắm đến là $(k_1, …, k_n, ?_A, X*?_B)$

Vậy $?_A, ?_B$ là gì:

• $?_A$: Ta mong muốn LLL sẽ chỉ sử dụng 1 bội số cho hàng đầu tiên $\to$ chọn $?_A = 2^{128}$. Điều này sẽ “thuyết phục” LLL rằng vector này đã đủ lớn và không sử dụng quá nhiều bội số cho hàng này.
• $?_B$: Ta sẽ không muốn $X?_B$ lớn hơn rất nhiều so với phần còn lại của vector vì khi đó vector mà ta nhắm đến không còn “nhỏ” nữa. $X*?_B$ nên có khoảng $128 bit$ $\to$ $?_B$ = $2^{-6}$

Sau khi chọn những giá trị này, chúng ta có thể xây dựng ma trận và áp dụng LLL. Chúng ta sẽ tìm một hàng mà cột thứ hai từ cuối là $\pm2^{128}$, và giả định rằng hàng đó tương ứng với $k_i$ cần tìm.